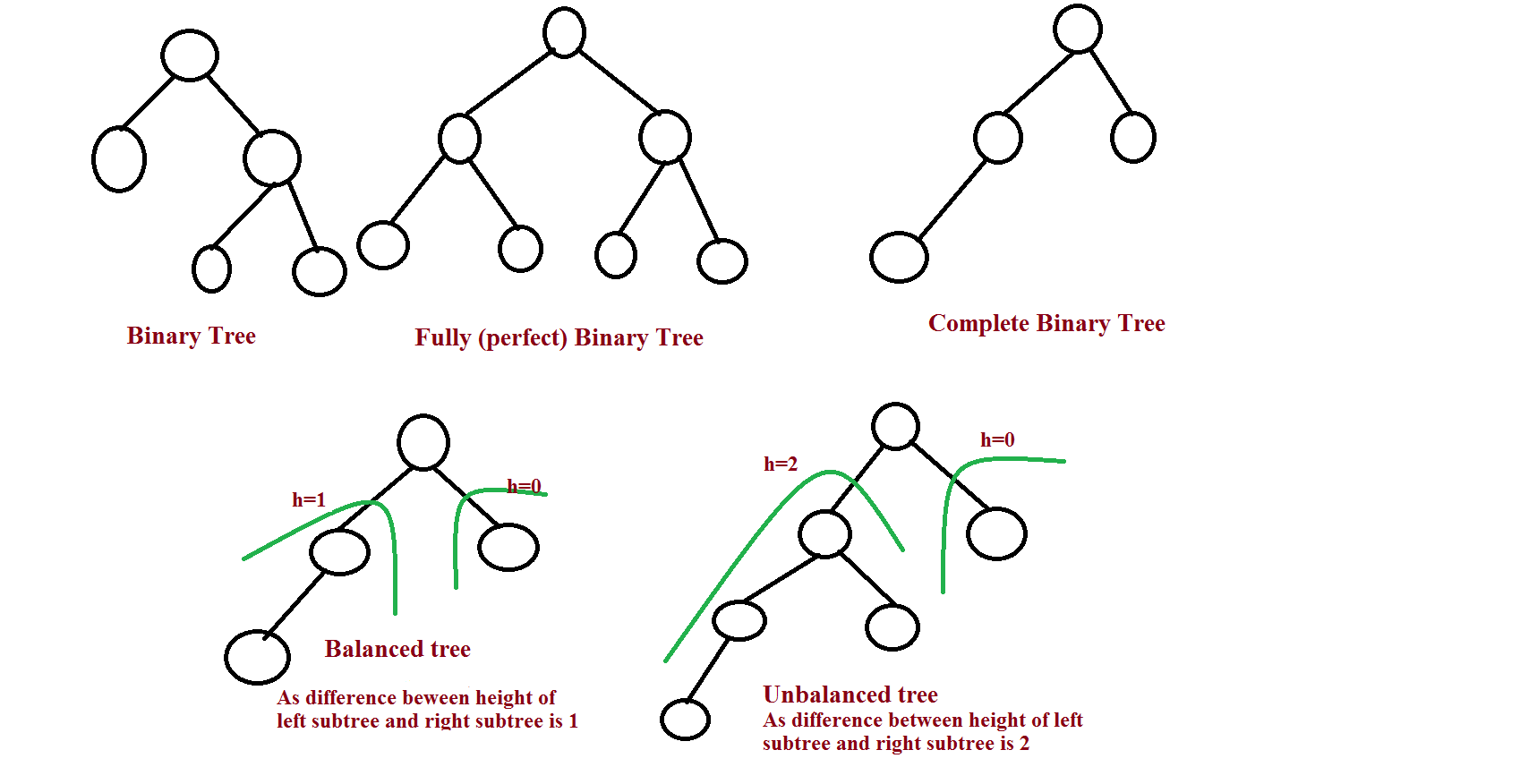
BINARY TREE

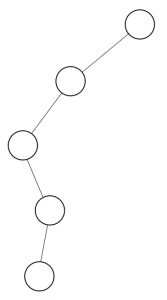 <skewed Binary tree

• Node at the top is called as root.
• A line connecting the parent to the child is edge.
• Nodes that do not have children are called leaf.
• Nodes that have the same parent are called sibling.
• Degree of node is the total sub tree of the node.
• Height/Depth is the maximum degree of nodes in a tree.
• If there is a line that connects p to q, then p is called the ancestor of q, and q is a descendant of p.

 

• Binary tree is a rooted tree data structure in which each node has at most two children.

There are 4 types of Binary Tree:

• Perfect Binary Tree
• Complete Binary Tree
• Skewed Binary Tree and
• Balanced Binary Tree

 

• Each Node of a binary tree has a maximum of 2 childs.

Perfect :

• This Binary Tree has the same depth for every level

Complete:

• This Binary Tree is almost perfect except the last level.
• Perfect Binary tree is also a Complete Binary tree

Skewed :

• Every level only has one node.

Balanced :

• binary tree in which no leaf is much farther away from the root than any other leaf (different balancing scheme allows different definitions of “much farther”).

Properties of Binary Tree

• Every level of the binary tree, has its own maximum nodes.
• Those levels start from 0.
• In level 0, maximum 1 node.
• In level k, maximum 2^k nodes.

How to count the maximum nodes in a tree according to its height:

height -> 2^(h+1) – 1

Maximum nodes in binary tree of height 3 is

2^4 – 1 = 15

Maximum height = n-1

Minimum height = 2log(n)

Sources : Binus University